In last week’s exploration we uncovered many equilateral triangles hiding in a general triangle ABC. This week we’ll find circles.

Draw any triangle ABC. The line AH_A perpendicular to BC is called the altitude though A, with H_A at the foot of the altitude. (See the image below.) It can be shown that the three altitudes AH_A, BH_B, and CH_C meet at a single point, H, called the orthocenter of triangle ABC.

Now, let’s put dots at a few important points on our triangle: First, dot the three altitude feet, H_A, H_B, and H_C. Next, dot the midpoints of the sides of the triangle, which we’ll call M_A, M_B, and M_C. Finally, dot the Euler points E_A, E_B, and E_C, which are halfway between H (the orthocenter) and the vertices of our triangle. Today’s first miracle is that all nine of these dots lie on a single circle, aptly named the 9-point circle:

Recall that it only takes three points to determine a circle, so nine on a single circle is very far from coincidence!

Another way to coax a circle out of triangle ABC is to “inscribe” one in the triangle by drawing a circle tangent to the three sides. This circle is called the incircle. Our second miracle is that the incircle and the 9-point circle, which were constructed in very different ways, nevertheless play nicely together: they are tangent! The point where they touch is known as the Feuerbach point of triangle ABC, named after Karl Feuerbach who discovered and proved this difficult fact in 1822.

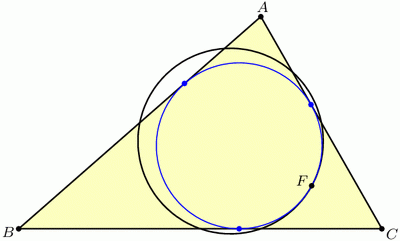
But there are three other circles that, like the incircle, are tangent to all three lines of the triangle. These “exscribed” circles are called the excircles of triangle ABC, and as luck (or extraversions^[1]) would have it, these are also tangent to the 9-point circle:

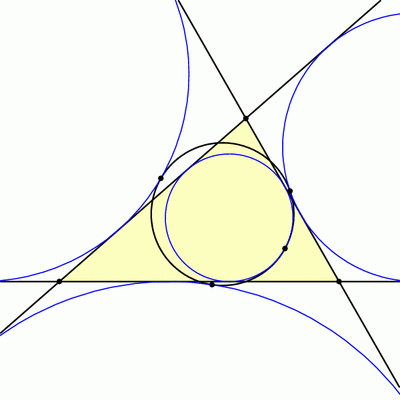
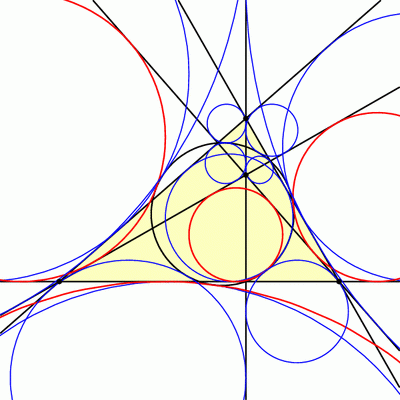
But wait, there’s more! It turns out that triangles ABC and HBC have the same 9-point circle, and so if we look at the incircle and excircles of triangle HBC, these will also be tangent to our 9-point circle. The same is true for triangles HCA and HAB, so we have found 16 circles all tangent to the nine-point circle!

Notes

1. Recall that we used extraversions last week to go from one Morley triangle to another. Here, extraversions interchange the incircle and excircles. [↩]