Let’s play a game; just the two of us. We’ll need a (potentially large!) chess board and a single queen somewhere on the board. We take turns making queen moves, always making progress toward the bottom-left corner of the board. Specifically, in one turn we are allowed to move the queen as far as we want either straight down, straight left, or diagonally down and left (at a 45-degree angle). The first to land the queen on the bottom-left corner wins the game. If you go first and we both play as best as possible, who wins? Well, it depends on where the queen started.
If the queen starts at any of the light-red spaces in the diagram below, you can win on the first move by going straight to the bottom-left corner. On the other hand, if the queen starts at (2,1), then you’re sunk: any move you make lands on a red square and so leaves me in a position to win. So (2,1) is a losing position, indicated by dark blue shading. (The jagged edge reminds us that we could ask the same questions on much bigger grids.)
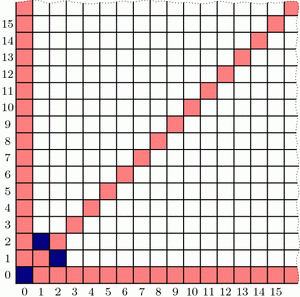
What should you do if the queen starts at, say, (6,5)? Move to (2,1)! This leaves me in a losing position, so no matter how I respond, you’ll win. So once we find where all the blue losing cells are, your strategy should be: always move to a blue cell, if you can. What if you can only land on red cells? Then you must have started at a blue position, and you’re going to lose.
This also tells us how to find the losing positions, step by step. We know that (2,1) and (1,2) are losing positions, so any position that can reach these in one move is a winning position. But now (3,5) and (5,3) can only reach red cells, so they are blue, and in turn, anything that can directly reach (3,5) or (5,3) is red.

Continuing like this, we can fill up our board as follows:
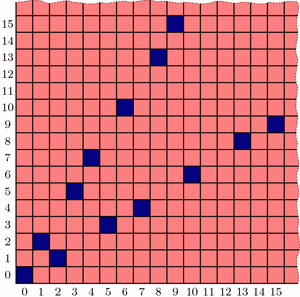
Interestingly, the blue positions seem to fit nicely into two straight lines forming a “V”-shape, but the exact pattern governing their placement is less clear (especially if we were to ask about larger grids!). Is there more underlying structure in the blue cells’ positioning?[1] How could we discover the pattern in their placement? And why does that line seem to have slope equal to the golden ratio, \(\phi = (1+\sqrt{5})/2\)?[2] Tune in next week to find out! In the meantime, be sure to play a few rounds of Wythoff’s game with your friends!
Yesterday I posted a small essay, which was not easy to understand since I missed one line. Today I try again to express myself:
Build up piles of chips in a row from left to right. The height (that ist the number of chips in a pile) is given by an integer. We start a solitary game with a row of piles from left to right 1 2 3 4 5 6
Now we lift the leftmost pile and put it on it‘s right neighbour:
3 3 4 5 6
From now on, wie always lift the leftmost pile and put it one by one and pile by pile to he right neighboured piles:
4 5 6 6
If there is no pile to put a chip on but still chips remaining to distribute, you built piles of one-chip-height: 6 7 7 1
Each move of he game means lifting the leftmost pile and distribute it’s chips one by one either on the right neighboured piles or you built piles of one-chip-height. You end the game when you reach the mirrored starting cassembly
6 5 4 3 2 1
Don‘t forget to count the number of moves. Play the game with other starting assemblies i.e. 1 2 3 or 1 2 3 4 and and establish a lookup table:
Number of piles in the starting assembly 1 2 3 4 5 6 7 8
Number of moves to mirror this assembly
Which sequence is obtained?
As I mentioned at Brent’s blog, my first encounter with this was through Paul Zeitz’s puppies and kittens game: The two players come in turns to the pet store, and each time have to buy at least one pet. The rules are that they can buy: * As many puppies as they want, or * As many kittens as they want, or * An equal number of puppies and kittens.
I love this game, though i didn’t know it was “Wythoff’s Game.” I did this with my Algebra 2 class on the first day, but we just called it Corner the Queen.
Anyhow, can’t wait to hear what’s coming next weak!
Corner the Queen? I like that name. Thanks!
I have also heard the title “Wythoff’s Nim”, since the x- and y-coordinates behave like a modified, two-pile game of Nim. (More confusing if you don’t know Nim, of course.)