Last time we discussed some rather challenging holes of (mathematical) mini-golf, uncovering Tokarski’s construction of some un-hole-in-one-able holes. By contrast, here is the all-time easiest hole of mini-golf, namely, a guaranteed hole-in-one:

By some miracle of geometry, if we take an ellipse (i.e., a stretched or squashed circle) and place the ball and cup at two special points \(F_1\) and \(F_2\) called the foci of the ellipse, then any golf shot leaving \(F_1\) will bounce off a wall and proceed directly to \(F_2\).^[1] You can’t miss!^[2]

Curiously, this easiest golf hole can be used to construct some even more challenging ones. For starters, consider a mushroom-shaped room as illustrated below (left), where the “mushroom head” is half of an ellipse with foci \(F_1\) and \(F_2\). Then the same reflection principle mentioned above tells us that any shot entering the mushroom head via segment \(F_1F_2\) will be reflected straight back through \(F_1F_2\) and sent back down the stem. This means that no shot from P can ever reach the triangular “fang” containing Q, and in particular, no hole-in-one from P to Q is possible. In the mirrored-room setting (described last time), if a light source is placed at P, then the whole triangular fang remains unilluminated! This is stronger than Tokarski’s room, where only a single point remained unlit. Similar constructions are possible even with rooms that have no corners^[3], such as the “curvy” mushroom on the right.

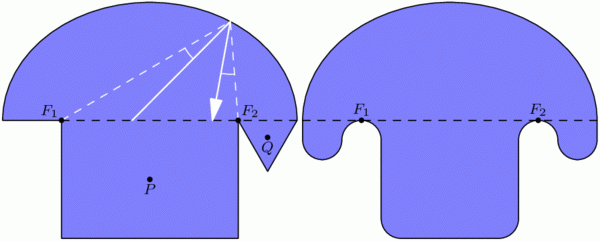
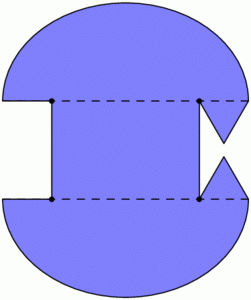
With this idea, we can construct a mirrored room that has dark patches no matter where a light bulb is placed. In the image below, if a light source is placed anywhere in the top half of the room, the lower triangular “fang” will be completely dark. Similarly, the upper fang is not illuminated from anywhere in the bottom half of the room. This room (or one quite like it) was originally designed by Roger Penrose in 1958.

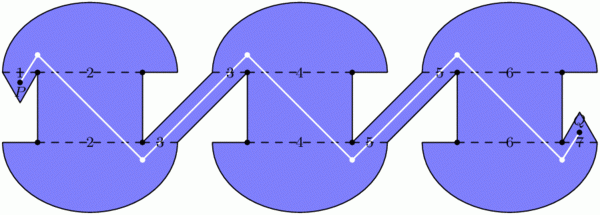
Back in the mini-golf setting, we can do something even more devious: by chaining multiple Penrose rooms together, we can construct golf holes that require as many shots as we wish! The golf hole below cannot be completed with fewer than 7 shots. Indeed, no single shot can cross two dashed segments with different numbers, so 7 shots are required.^[4]

What about polygons?

The golf holes last time were all polygons, whereas we have allowed curved boundaries here. Can we construct a polygonal golf hole, using only flat walls, that still requires at least 7 shots? Or even 3? Unfortunately, the answer this time is “we don’t know, but we think not.” In particular, it has been conjectured that, no matter where the ball and cup are placed in a polygonal golf hole, a single shot can place the ball as close to the hole as desired, so a short second putt can finish the job.^[5]

Notes

1. In fact, even more is true: all of these paths from \(F_1\) to \(F_2\) have the same length! We will not prove these facts today. [↩]
2. Assuming you hit hard enough, of course. [↩]
3. For the analysts out there, the room’s boundary can be made smooth. [↩]
4. This too can be accomplished with smooth boundary. [↩]
5. More strongly, O’Rourke and Petrovici conjecture that with a single light source in a polygonal room, the set of unilluminated points has measure 0. Reference: Joseph O’Rourke and Octavia Petrovici. Narrowing Light Rays with Mirrors. Proceedings of the 13th Canadian Conference on Computational Geometry, 137–140, 2001. [↩]