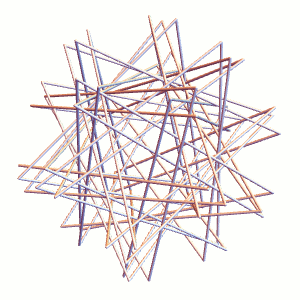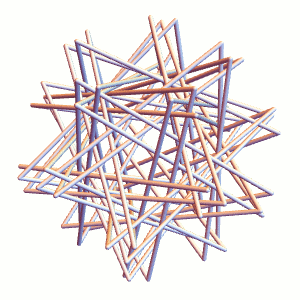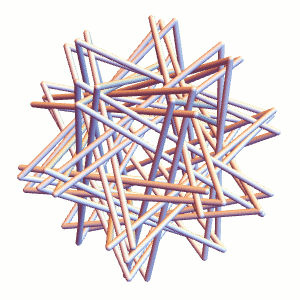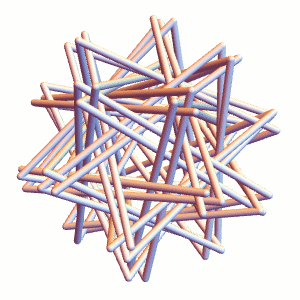[This is post #6 in a mini-blog-post series for NaBloPoMo 2015. Jump to the first, previous, or next post.]

So how could we compute/visualize the “perfect” length to diameter ration? Let’s start with a smaller, simpler thingy made of straws (not to be confused with Straws Thingy itself):

And here’s finding the tight, optimal packing:

The tubes are inflating (or equivalently, shortening) while pushing away from each other. When they can’t inflate(shrink) any more, we’ve reached the ideal, tight packing.

We can do the same for Straws Thingy proper (it’s a bit more difficult to see, hence the example above):

The resulting tight packing has a length to diameter ratio of about 27.43, according to my Mathematica simulation. Why does this look so different from the 23 and change from yesterday? They are measuring slightly different things:

The 27.43 refers to the edge length of the “axial” equilateral triangle, whereas the straws “shortcut” these corners via flexy bits. Of course, the exact shortcut dimensions vary from brand to brand, which further explains why I didn’t offer more precision to yesterday’s 23-or-24 measurement.

OK! It’s time to switch focus away from discussing Straws Thingy‘s geometry and toward learning, step by step, how to make your own! So go out, find those straws, and get ready for some excitement!