Category Archives: Math History

Chess, Bored

Counting/Probability, Games/Experiments, Math History, , ,

[This is post #3 in a series on the Thue-Morse sequence, which was introduced two weeks ago and discussed further last week.]

While the Thue-Morse sequence appears in many branches of Mathematics[1], this sequence has also captured a place in the history of chess.

With only the basic rules of chess (specifically, how pieces move and capture and how a game may end by checkmate or stalemate), there is no guarantee that a game of chess will ever finish. For example, two (very bored!) players could theoretically move their knights back and forth ad infinitum without ever engaging each other or capturing a piece (but why would they want to?). A more realistic example is drawn below. In this game, black will soon checkmate white if given the freedom to move, and white has no way to win. However, white can avoid losing by keeping black in an unending runaround with repeated checks, as illustrated. In this case (a phenomenon known as perpetual check), forcing an infinite game is more advantageous for white than allowing an otherwise inevitable loss.

Perpetual Check
Animation frames were made with the WiseBoard Chess Board Editor.

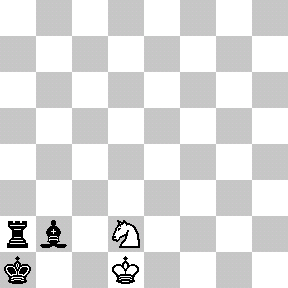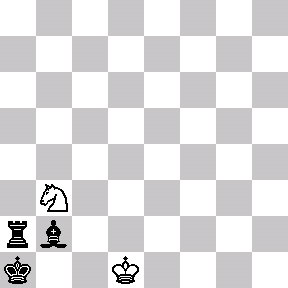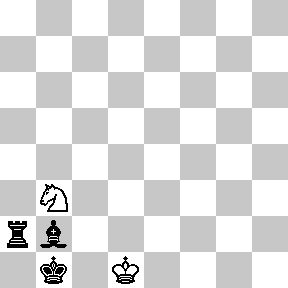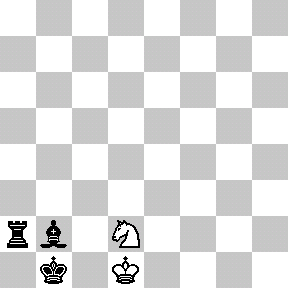
Because of this possibility of never finishing, a search began for new chess rules to guarantee that every game of chess eventually ends. One suggested rule was:

A chess game ends with a draw if a sequence of moves—with all pieces in exactly the same positions—is played three times successively.[2]

The hope was that any sufficiently long chess game would eventually repeat itself enough to break this rule. However, as Mathematician and Chess Grandmaster Max Euwe showed in 1929[3], this hope is not correct. Indeed, there exist infinite chess games that never repeat the same block of moves three times in a row!

How did he prove this? With the Thue-Morse Sequence, of course! He proved the very unintuitive fact that the Thue-Morse sequence has no chunk repeated three times consecutively. Such a thrice-repeated sequence is called a cube, so this property can be restated by saying that the Thue-Morse sequence is cube-free. For example, you will never find the sequences 1 1 1 or 011 011 011 in the Thue-Morse sequence. (Challenge: show that these two sequences do not appear. Harder challenge: show that the Thue-Morse sequence is cube free!) So, if the “very bored” knight-flippers described above decide to move their right knights or left knights according to the 1s and 0s of the Thue-Morse sequence, the resulting game will have no tripled move sequences.

Luckily, the above rule is not part of the current official chess rule set. There are now two rules on the books that can be used to eventually end any chess game. (In fact, either one would suffice. [Prove this!]) A draw may be declared in either of these situations:

  • The exact same board position appears three times ever during a game. (Every detail must be the same, such as whose turn it is, which kings have the ability to castle, etc.)
  • No pawn is moved and no piece is captured in 50 consecutive turns. (A turn consists of one move by each player.)

However, there’s (always) a catch. These two rules only take effect if a player notices and decides to declare a draw. So even with all modern rules in effect, the bored knight-flippers are still allowed to play their infinite game of chess—cube-free or not.

Notes

  1. A great survey called The ubiquitous Prouhet-Thue-Morse sequence by Allouche and Shallit documents many sightings of this sequence throughout Mathematics, including Combinatorics, Differential Geometry, Number Theory, Analysis, and as discussed here, Combinatorial Game Theory. [↩]
  2. Manfred Börgens, Max Euwe’s sequence [↩]
  3. in his paper titled Mengentheoretische Betrachtungen über das Schachspiel [↩]

Archimedes’ Circular Reasoning

Calculus/Analysis, Geometry, Math Foundations, Math History, Proofs, Trigonometry, , , ,

Every geometry textbook has formulas for the circumference (\(C = 2 \pi r\)) and area (\(A = \pi r^2\)) of a circle. But where do these come from? How can we prove them?

Well, the first is more a definition than a theorem: the number \(\pi\) is usually defined as the ratio of a circle’s circumference to its diameter: \(\pi = C/(2r)\). Armed with this, we can compute the area of a circle. Archimedes’ idea (in 260 BCE) was to approximate this area by looking at regular \(n\)-sided polygons drawn inside and outside the circle, as in the diagram below. Increasing \(n\) gives better and better approximations to the area.

Approximating circle area with triangles
The n-sided regular polygons inside (blue) and outside (red) a circle can be used to approximate the area of the circle. Shown here for n=12.

Look first at the inner polygon. Its perimeter is slightly less than the circle’s circumference, \(C = 2 \pi r\), and the height of each triangle is slightly less than \(r\). So when reassembled as shown, the triangles form a rectangle whose area is just under \(C/2\cdot r = \pi r^2\). Likewise, the outer polygon has area just larger than \(\pi r^2\). As \(n\) gets larger, these two bounds get closer and closer to \(\pi r^2\), which is therefore the circle’s area.

Archimedes used this same idea to approximate the number \(\pi\). Not only was he working by hand, but the notion of “square root” was not yet understood well enough to compute with. Nevertheless, he was amazingly able to use 96-sided polygons to approximate the circle! His computation included impressive dexterity with fractions: for example, instead of being able to use \(\sqrt{3}\) directly, he had to use the (very close!) approximation \(\sqrt{3} > 265/153\). In the end, he obtained the bounds \( 3\frac{10}{71} < \pi < 3\frac{1}{7} \), which are accurate to within 0.0013, or about .04%. (In fact, he proved the slightly stronger but uglier bounds \(3\frac{1137}{8069} < \pi < 3\frac{1335}{9347}\). See this translation and exposition for more information on Archimedes’ methods.)

These ideas can be pushed further. Focus on a circle with radius 1. The area of the regular \(n\)-sided polygon inscribed in this circle can be used as an approximation for the circle’s area, namely \(\pi\). This polygon has area \(A_n = n/2 \cdot \sin(360/n)\) (prove this!). What happens when we double the number of sides? The approximation changes by a factor of $$\frac{A_{2n}}{A_n} = \frac{2\sin(180/n)}{\sin(360/n)} = \frac{1}{\cos(180/n)}.$$ Starting from \(A_4 = 2\), we can use the above formula to compute \(A_8,A_{16},A_{32},\ldots\), and in the limit we find that $$\pi = \frac{2}{\cos(180/4)\cdot\cos(180/8)\cdot\cos(180/16)\cdots}.$$ Finally, recalling that \(\cos(180/4) = \cos(45) = \sqrt{\frac{1}{2}}\) and \(\cos(\theta/2) = \sqrt{\frac{1}{2}(1+\cos\theta)}\) (whenever \(\cos(\theta/2) \ge 0\)), we can rearrange this into the fun infinite product $$\frac{2}{\pi} = \sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}} \cdot \sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}}} \cdots$$ (which I found at Mathworld). (It’s ironic that this formula for a circle uses so many square roots!)

Kissing Spheres

Geometry, Math History, , , ,

If you put a quarter flat on a table, you can surround it with six other quarters that all touch the original. Is this the best you can do, if the coins can’t overlap? Well, yes: the coins are packed as tightly as possible, so there is no room for a seventh coin to fit around the middle one. We call this the Kissing Number Problem, and it gets much more interesting if you jump from two dimensions to three: given a sphere of radius 1, how many nonoverlapping spheres (of radius 1) can you place around it such that they all “kiss” the original sphere? Said differently, what is the kissing number in 3 dimensions?

Here’s a pretty good attempt: If you put one sphere at each vertex of a cuboctahedron like this,

Twelve spheres all kissing a central (blue) sphere and arranged at the vertices of a cuboctahedron.
Twelve spheres all kissing a central (blue) sphere and arranged at the vertices of a cuboctahedron.

you’ll end up with 12 that seem pretty tightly packed. In another try, you could put a sphere at each vertex of an icosahedron:

Twelve spheres all kissing a central (blue) sphere and arranged at the vertices of an icosahedron.
Twelve spheres all kissing a central (blue) sphere and arranged at the vertices of an icosahedron.

You’ll again get 12, but this time there is noticable wiggle room to move the spheres without losing contact with the central sphere—so much wiggle room, in fact, that any two spheres can switch places! Is there enough extra space for a 13th sphere to fit? This was a topic of heated debate between Isaac Newton and David Gregory (who believed 12 and 13, respectively), but it was not resolved until much later, in 1953, in favor of Newton’s 12. The proof is highly nontrivial.

What about still higher dimensions? What is the kissing number in four dimensions? (What does a 4-dimensional sphere even look like? Perhaps a topic of a future post…) This too is known, and the answer is 24—the proof is again quite difficult. See if you can figure out the arrangement! What about dimension 5, 6, 7, … ? As might be expected, the problem gets even harder in higher dimensions, and no other exact kissing numbers are known—except for two. Due to some veritable mathematical miracles (namely, the highly symmetric structures called the E8 lattice and the Leech lattice), the kissing numbers in dimensions 8 and 24 have been shown to be 240 and 196560, respectively.