Tag Archives: chess

Wythoff’s Game: Red or Blue?

Counting/Probability, Games/Experiments, , ,

Let’s play a game; just the two of us. We’ll need a (potentially large!) chess board and a single queen somewhere on the board. We take turns making queen moves, always making progress toward the bottom-left corner of the board. Specifically, in one turn we are allowed to move the queen as far as we want either straight down, straight left, or diagonally down and left (at a 45-degree angle). The first to land the queen on the bottom-left corner wins the game. If you go first and we both play as best as possible, who wins? Well, it depends on where the queen started.

If the queen starts at any of the light-red spaces in the diagram below, you can win on the first move by going straight to the bottom-left corner. On the other hand, if the queen starts at (2,1), then you’re sunk: any move you make lands on a red square and so leaves me in a position to win. So (2,1) is a losing position, indicated by dark blue shading. (The jagged edge reminds us that we could ask the same questions on much bigger grids.)

Wythoff's game: beginning analysis
If the queen starts on a light-red cell, you win on the first move. If she starts on (1,2) or (2,1) (dark blue), you lose.

What should you do if the queen starts at, say, (6,5)? Move to (2,1)! This leaves me in a losing position, so no matter how I respond, you’ll win. So once we find where all the blue losing cells are, your strategy should be: always move to a blue cell, if you can. What if you can only land on red cells? Then you must have started at a blue position, and you’re going to lose.

This also tells us how to find the losing positions, step by step. We know that (2,1) and (1,2) are losing positions, so any position that can reach these in one move is a winning position. But now (3,5) and (5,3) can only reach red cells, so they are blue, and in turn, anything that can directly reach (3,5) or (5,3) is red.

Wythoff's game: continued analysis
Finding blue cells step by step. Left: Because (1,2) and (2,1) are blue, any cells that can reach these directly are red. Right: (3,5) and (5,3) can only reach red cells, so we color them blue. This reveals even more red cells.

Continuing like this, we can fill up our board as follows:

Wythoff's game: completed analysis
Continuing step-by-step as above, all blue cells in the grid are revealed. What patterns can we find?

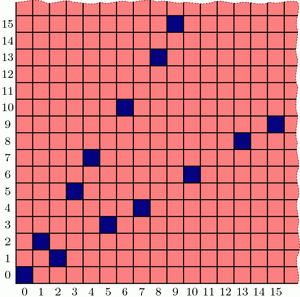
Interestingly, the blue positions seem to fit nicely into two straight lines forming a “V”-shape, but the exact pattern governing their placement is less clear (especially if we were to ask about larger grids!). Is there more underlying structure in the blue cells’ positioning?[1] How could we discover the pattern in their placement? And why does that line seem to have slope equal to the golden ratio, \(\phi = (1+\sqrt{5})/2\)?[2] Tune in next week to find out! In the meantime, be sure to play a few rounds of Wythoff’s game with your friends!

Notes

  1. Yes. We call that a leading question… [↩]
  2. Correction: that is a leading question. [↩]

Chess, Bored

Counting/Probability, Games/Experiments, Math History, , ,

[This is post #3 in a series on the Thue-Morse sequence, which was introduced two weeks ago and discussed further last week.]

While the Thue-Morse sequence appears in many branches of Mathematics[1], this sequence has also captured a place in the history of chess.

With only the basic rules of chess (specifically, how pieces move and capture and how a game may end by checkmate or stalemate), there is no guarantee that a game of chess will ever finish. For example, two (very bored!) players could theoretically move their knights back and forth ad infinitum without ever engaging each other or capturing a piece (but why would they want to?). A more realistic example is drawn below. In this game, black will soon checkmate white if given the freedom to move, and white has no way to win. However, white can avoid losing by keeping black in an unending runaround with repeated checks, as illustrated. In this case (a phenomenon known as perpetual check), forcing an infinite game is more advantageous for white than allowing an otherwise inevitable loss.

Perpetual Check
Animation frames were made with the WiseBoard Chess Board Editor.

Because of this possibility of never finishing, a search began for new chess rules to guarantee that every game of chess eventually ends. One suggested rule was:

A chess game ends with a draw if a sequence of moves—with all pieces in exactly the same positions—is played three times successively.[2]

The hope was that any sufficiently long chess game would eventually repeat itself enough to break this rule. However, as Mathematician and Chess Grandmaster Max Euwe showed in 1929[3], this hope is not correct. Indeed, there exist infinite chess games that never repeat the same block of moves three times in a row!

How did he prove this? With the Thue-Morse Sequence, of course! He proved the very unintuitive fact that the Thue-Morse sequence has no chunk repeated three times consecutively. Such a thrice-repeated sequence is called a cube, so this property can be restated by saying that the Thue-Morse sequence is cube-free. For example, you will never find the sequences 1 1 1 or 011 011 011 in the Thue-Morse sequence. (Challenge: show that these two sequences do not appear. Harder challenge: show that the Thue-Morse sequence is cube free!) So, if the “very bored” knight-flippers described above decide to move their right knights or left knights according to the 1s and 0s of the Thue-Morse sequence, the resulting game will have no tripled move sequences.

Luckily, the above rule is not part of the current official chess rule set. There are now two rules on the books that can be used to eventually end any chess game. (In fact, either one would suffice. [Prove this!]) A draw may be declared in either of these situations:

  • The exact same board position appears three times ever during a game. (Every detail must be the same, such as whose turn it is, which kings have the ability to castle, etc.)
  • No pawn is moved and no piece is captured in 50 consecutive turns. (A turn consists of one move by each player.)

However, there’s (always) a catch. These two rules only take effect if a player notices and decides to declare a draw. So even with all modern rules in effect, the bored knight-flippers are still allowed to play their infinite game of chess—cube-free or not.

Notes

  1. A great survey called The ubiquitous Prouhet-Thue-Morse sequence by Allouche and Shallit documents many sightings of this sequence throughout Mathematics, including Combinatorics, Differential Geometry, Number Theory, Analysis, and as discussed here, Combinatorial Game Theory. [↩]
  2. Manfred Börgens, Max Euwe’s sequence [↩]
  3. in his paper titled Mengentheoretische Betrachtungen über das Schachspiel [↩]