Given my blog title, how have I gone this long without discussing triangle geometry? I will rectify this gross negligence in the next few weeks. Let’s begin with a seemingly impossible fact due to Frank Morley.
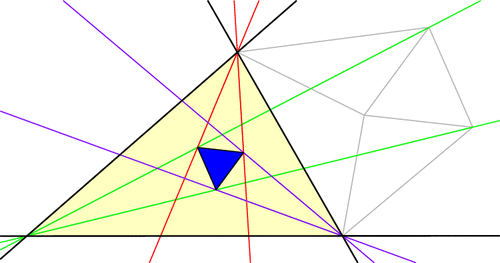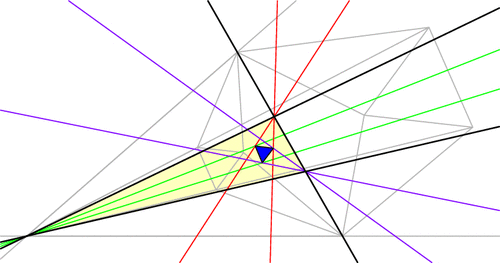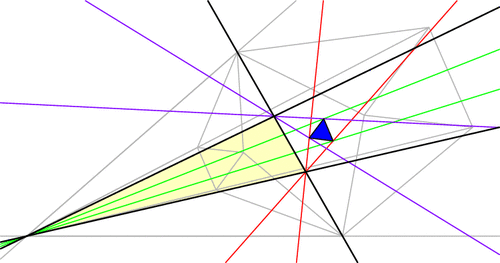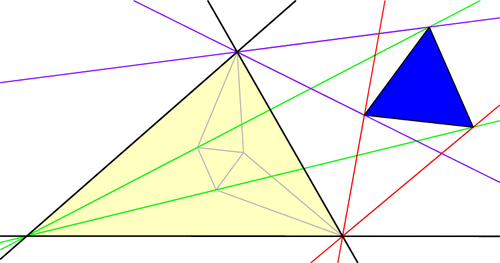
Start with a triangle ABC, with any shape you wish. Now cut its angles into three equal parts, and extend these angle trisectors until they meet in pairs as illustrated below, forming triangle PQR. Morley’s amazing theorem says that this Morley triangle, PQR, will always be equilateral!
Why would this be true? Well, Morley’s theorem tells us that this diagram has three nice 60-degree angles in the middle, but we may suspect that, in fact, all of the angles are nice! This key insight lets us piece together the following argument, where we build up the diagram backwards from its constituent pieces. Draw seven separate “puzzle piece” triangles with angles and side-lengths as shown below, where the original triangle ABC has angles \(3\alpha,3\beta,3\gamma\) respectively. (Be sure to check that puzzle pieces with these specifications actually exist! Hint: use the Law of Sines.)

Now, fit the pieces together: all matching edge-lengths are equal (by design), and the angles around vertex P add up to \(60+(\gamma+60)+(\alpha+120)+(\beta+60)=360\) and similarly for Q and R, so the puzzle fits together into a triangle similar to our original triangle ABC. But now these pieces must make up the Morley configuration, and since we started with an equilateral in the middle, we’re done with the proof![1]
But there’s more to the Morley story. Let’s push A and C to make them swap positions, dragging the trisectors and Morley triangle along for the ride (a process known as extraversion). We end up using some external angle trisectors instead of only internal ones, but the Morley triangle remains equilateral throughout. This gives us a new equilateral Morley triangle for our original ABC!
In fact, each vertex of ABC has six angle trisectors (three pairs of two), and if you continue applying extraversions you’ll soon uncover that our original triangle ABC has 18 equilateral Morley triangles arranged in a stunning configuration! (Click for larger image.)
Here’s a challenge: the diagram above has 27 equilateral triangles, but only 18 of them are Morley triangles (i.e., are made from a pair of trisectors from each vertex). Which ones are they?
Notes
- This is a slight modification of a proof by Conway and Doyle. [↩]