Tag Archives: Morley’s theorem

Three-Cornered Deltoids

Geometry, , , , ,

[This is the third and final post in this series on triangle geometry. See the previous posts on Morley’s theorem and the 9-point circle.]

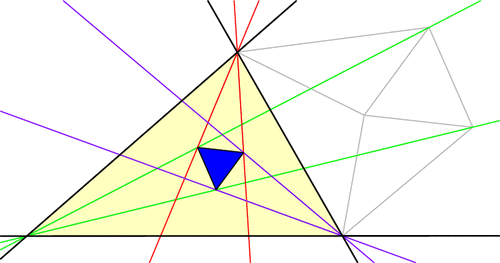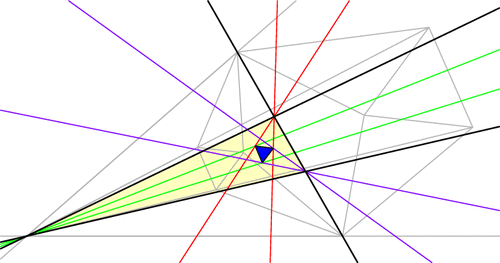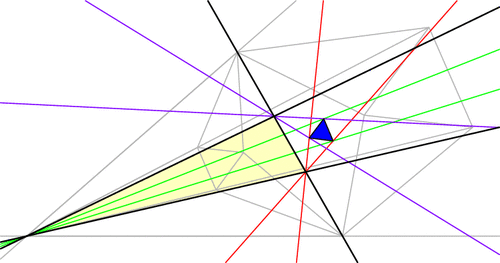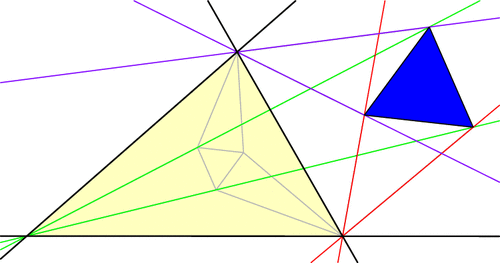
For our final exploration in this series, let’s again begin with our triangle ABC and a point P on the circumcircle of the triangle, i.e., the circle through the three vertices. If we drop P directly onto the three lines of the triangle at right angles[1], then by coincidence, these three points lie on a single line, called the Simson line of point P.

The Simson line of point P in triangle ABC

Just for fun, let’s draw point Q diametrically opposite from P on the circumcircle, and let’s also look at Q‘s Simson line. How do these two Simson lines interact? Somewhat surprisingly, these lines intersect at right angles. The phenomenal part is that this point of intersection lies on the 9-point circle!

Two opposite Simson lines

Furthermore, as P and Q move around the circumcircle, the intersection of their Simson lines moves around the 9-point circle at twice the speed and in the opposite direction:

Simson lines tracing the 9-point circle

This story gets even more unbelievable when we look at how the Simson lines move in this animation. As it turns out, the Simson lines trace a curve in the shape of a deltoid, which is like an equilateral triangle with curved sides[2]. The deltoid traced here is called Steiner’s deltoid.

Simson lines trace the Steiner deltoid

And finally, here’s an incredible fact that ties everything together: If we draw the equilateral triangle around this deltoid, then the edges are parallel to the edges of the equilateral Morley triangle(s).

Steiner deltoid and Morley triangle

Holy Morley!

Notes

  1. Note that we may have to extend the lines beyond the triangle. [↩]
  2. Specifically, a deltoid is the shape that results when you roll a circle inside a circle three-times larger and trace the path of a single point. See Wikipedia:Deltoid_curve for more information. [↩]

Many Morley Triangles

Geometry, Proofs, , ,

Given my blog title, how have I gone this long without discussing triangle geometry? I will rectify this gross negligence in the next few weeks. Let’s begin with a seemingly impossible fact due to Frank Morley.

Start with a triangle ABC, with any shape you wish. Now cut its angles into three equal parts, and extend these angle trisectors until they meet in pairs as illustrated below, forming triangle PQR. Morley’s amazing theorem says that this Morley triangle, PQR, will always be equilateral!

Morley's theorem

Why would this be true? Well, Morley’s theorem tells us that this diagram has three nice 60-degree angles in the middle, but we may suspect that, in fact, all of the angles are nice! This key insight lets us piece together the following argument, where we build up the diagram backwards from its constituent pieces. Draw seven separate “puzzle piece” triangles with angles and side-lengths as shown below, where the original triangle ABC has angles \(3\alpha,3\beta,3\gamma\) respectively. (Be sure to check that puzzle pieces with these specifications actually exist! Hint: use the Law of Sines.)

Proof of Morley's theorem
Triangle ABC is built out of seven "puzzle pieces" with angles and side-lengths as specified here. In this diagram, \(\alpha^\prime=\alpha+60\) and \(\alpha^{\prime\prime}=\alpha+120\), and similarly for \(\beta\) and \(\gamma\).

Now, fit the pieces together: all matching edge-lengths are equal (by design), and the angles around vertex P add up to \(60+(\gamma+60)+(\alpha+120)+(\beta+60)=360\) and similarly for Q and R, so the puzzle fits together into a triangle similar to our original triangle ABC. But now these pieces must make up the Morley configuration, and since we started with an equilateral in the middle, we’re done with the proof![1]

But there’s more to the Morley story. Let’s push A and C to make them swap positions, dragging the trisectors and Morley triangle along for the ride (a process known as extraversion). We end up using some external angle trisectors instead of only internal ones, but the Morley triangle remains equilateral throughout. This gives us a new equilateral Morley triangle for our original ABC!

New Morley triangles through extraversion

In fact, each vertex of ABC has six angle trisectors (three pairs of two), and if you continue applying extraversions you’ll soon uncover that our original triangle ABC has 18 equilateral Morley triangles arranged in a stunning configuration! (Click for larger image.)

All 18 Morley triangles

Here’s a challenge: the diagram above has 27 equilateral triangles, but only 18 of them are Morley triangles (i.e., are made from a pair of trisectors from each vertex). Which ones are they?

Notes

  1. This is a slight modification of a proof by Conway and Doyle. [↩]