Tag Archives: Wythoff’s game

Fibonacci-Based Arithmetic

Games/Experiments, Number Theory, ,

[This is the final Wythoff’s game post. See the previous ones here: #1, #2, #3, #4, #5, #6. We’ll have a few shorter, 1- or 2-post topics starting next week.]

In our standard, base-10 number system, each position represents a specific power of 10: the number 275 in base 10 means that I have five 1s, seven 10s, and two 100s. Similarly, in the base-2 system, each position represents a different power of 2: 10011 in base 2 says I have a 1, a 2, and a 16, but no 4s or 8s.[1] Instead of using powers of 10 or 2, what happens if we use Fibonacci numbers?

We can find the Fibonacci numbers by starting[2] at \(a_1=1\) and \(a_2=2\) and then computing each term as the sum of the two previous ones, \(a_n=a_{n-1}+a_{n-2}\):

1, 2, 3, 5, 8, 13, 21, 34, 55, …

Let’s use these as our position values in our so-called Fibonacci base, using just the digits 0 and 1. For example, 1010011F stands for \(a_7+a_5+a_2+a_1 = 21+8+2+1 = 32\).

Notice that \(a_2+a_1=a_3\), so we can write 32 instead as \(a_7+a_5+a_3\), meaning 32=1010100F. In much the same way, any time we have a Fibonacci representation of a number, we can repeatedly use the identity \(a_n=a_{n-1}+a_{n-2}\) to ensure that we never use consecutive Fibonacci numbers:

Theorem (Zeckendorf): Every positive integer can be expressed in base Fibonacci with no adjacent 1s. Furthermore, this representation is unique.

The “base-Fibonacci representation” of a number usually refers to its Zeckendorf representation as in this theorem. There’s a simple greedy method to find a number’s Zeckendorf representation: use the largest Fibonacci number less than (or equal to) your number, and repeat on the remainder. For example, to represent 46 in this way, check that the largest Fibonacci number below 46 is \(a_8=34\), leaving 12 as the remainder. The largest Fibonacci number below (or equal to) 12 is \(a_5=8\), with a remainder of 4. Now we have to use \(a_3=3\), and finally we’re left with \(1=a_1\). So \(46=a_8+a_5+a_3+a_1=10010101_F\) is the Zeckendorf representation of 46.

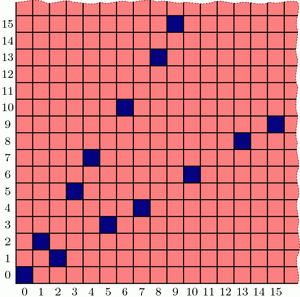
But why discuss base Fibonacci now? What does this have to do with Wythoff’s game? Zeckendorf representations provide another simple way to characterize the losing positions in Wythoff’s game! Here’s a beautiful result:

Theorem: If \(a \le b\) are positive integers, then \((a,b)\) and \((b,a)\) are losing position in Wythoff’s game precisely when:

  • The Zeckendorf representation of a ends in an even number of 0s, and
  • The Zeckendorf representation of b is the same as that of a except for one more 0 on the end.

For example, 11=10100F ends in two 0s (two is even), and 18=101000F has the same representation except for an extra 0 at the end, so (11,18) and (18,11) are Wythoff losing positions. Unlike the formula using multiples of \(\phi\) and \(\phi^2\) that we proved in the last few posts, this provides a method we could actually compute (without a calculator) on reasonably-sized grids when playing with friends (or enemies)! After all we’ve learned about Wythoff’s game, we finally have a way to win it!

Further Reading

Our Wythoff’s game saga is now ending here on Three-Cornered Things, but here are a few recommended resources if you wish to further explore this rich topic on your own:

Notes

  1. If these concepts are unfamiliar, see this previous post on number bases. [↩]
  2. Careful: these indices are shifted from the other common convention that starts the Fibonacci numbers at \(F_1=1\) and \(F_2=1\), which is why I’m using as instead of Fs. [↩]

Just Beatty It

Algebra, Proofs, , , , , ,

[This is the 6th post in the current series about Wythoff’s game: see posts #1, #2, #3, #4, and #5. Caveat lector: this post is a bit more difficult than usual. Let me know what you think in the comments!]

Our only remaining task from last week was to prove the mysterious Covering Theorem: we must show that there is exactly one dot in each row and column of the grid (we already covered the diagonal case). Since the rows and columns are symmetric, let’s focus on columns.

The columns really only care about the x-coordinates of the points, so let’s draw just these x-coordinates on the number-line. We’ve drawn \(\phi,2\phi,3\phi,\ldots\) with small dots and \(\phi^2,2\phi^2,3\phi^2,\ldots\) with large dots. We need to show that there’s exactly one dot between 1 and 2, precisely one dot between 2 and 3, just one between 3 and 4, and so on down the line. For terminology’s sake, break the number line into length-1 intervals [1,2], [2,3], [3,4], etc., so we must show that each interval has one and only one dot:

Multiples of phi and phi^2 on a number line
Multiples of \(\phi\) (small blue dots) and of \(\phi^2\) (large green dots) perfectly interleave the integers on the number line. This is proved below.

Why is this true? One explanation hinges on a nice geometric observation: Take any small dot s and large dot t on our number-line above, and cut segment st into two parts in the ratio \(1:\phi\) (with s on the shorter side). Then the point where we cut is always an integer! For example, the upper-left segment in the diagram below has endpoints at \(s=2\cdot\phi\) and \(t=1\cdot\phi^2\), and its cutting point is the integer 3:

Splitting blue and green dots at integers
When a segment formed by a small and a large dot is cut into a \(1:\phi\) ratio (closer to the small dot), the cutting point is always an integer. In fact, the segment between \(j\cdot \phi\) and \(k\cdot \phi^2\) is cut at the integer j+k.

In general, if s is the jth small dot—i.e., \(s=j\cdot\phi\)—and \(t=k\cdot\phi^2\) is the kth large dot, then the cutting point between s and t is \(\frac{1}{\phi}\cdot s+\frac{1}{\phi^2}\cdot t = j+k\) (Why?![1]). But more importantly, this observation shows that no interval has two or more dots: a small dot and a large dot can’t be in the same interval because they always have an integer between them![2]

So all we have to do now is prove that no interval is empty: for each integer n, some dot lies in the interval [n,n+1]. We will prove this by contradiction. What happens if no dot hits this interval? Then the sequence \(\phi,2\phi,3\phi,\ldots\) jumps over the interval, i.e., for some j, the jth dot in the sequence is less than n but the (j+1)st is greater than n+1. Likewise, the sequence \(\phi^2,2\phi^2,3\phi^2,\ldots\) jumps over the interval: its kth dot is less than n while its (k+1)st dot is greater than n+1:

Showing no interval is empty
Illustrating the hypothetical situation where interval [n, n+1] contains no dot. This is used in a proof by contradiction to show that the interval in fact cannot be empty.

By our observation above on segment \(s=j\phi\) and \(t=k\phi^2\), we find that the integer j+k is less than n, so \(j+k\le n-1\). Similarly, \(j+k+2 > n+1\), so \(j+k+2 \ge n+2\). But together these inequalities say that \(n\le j+k\le n-1\), which is clearly absurd! This is the contradiction we were hoping for, so the interval [n,n+1] is in fact not empty. This completes our proof of the Covering Theorem and the Wythoff formula!

It was a long journey, but we’ve finally seen exactly why the Wythoff losing positions are arranged as they are. Thank you for following me through this!

A Few Words on the Column Covering Theorem

Using the floor function \(\lfloor x\rfloor\) that rounds x down to the nearest integer, we can restate the Column Covering Theorem in perhaps a more natural context. The sequence of integers $$\lfloor\phi\rfloor = 1, \lfloor 2\phi\rfloor = 3, \lfloor 3\phi\rfloor = 4, \lfloor 4\phi\rfloor = 6, \ldots$$ is called the Beatty sequence for the number \(\phi\), and similarly, $$\lfloor\phi^2\rfloor = 2, \lfloor 2\phi^2\rfloor = 5, \lfloor 3\phi^2\rfloor = 7, \lfloor 4\phi^2\rfloor = 8,\ldots$$ is the Beatty sequence for \(\phi^2\). Today we proved that these two sequence are complementary, i.e., together they contain each positive integer exactly once. We seemed to use very specific properties of the numbers \(\phi\) and \(\phi^2\), but in fact, a much more general theorem is true:

Beatty’s Theorem: If \(\alpha\) and \(\beta\) are any positive irrational numbers with \(\frac{1}{\alpha}+\frac{1}{\beta}=1\), then their Beatty sequences \(\lfloor\alpha\rfloor, \lfloor 2\alpha\rfloor, \lfloor 3\alpha\rfloor,\ldots\) and \(\lfloor\beta\rfloor, \lfloor 2\beta\rfloor, \lfloor 3\beta\rfloor,\ldots\) are complementary sequences.

Furthermore, our same argument—using \(\alpha\) and \(\beta\) instead of \(\phi\) and \(\phi^2\)—can be used to prove the more general Beatty’s Theorem!

Notes

  1. Hint: use the identity \(\frac{1}{\phi}+\frac{1}{\phi^2}=1\). [↩]
  2. To be thorough, we should also check that no interval has two small or two large dots. Why can’t this happen? [↩]

Putting the Why in Wythoff

Counting/Probability, Games/Experiments, Proofs, ,

Last week we drew dots at multiples of the vectors \(v=(\phi,\phi^2)\) and \(w=(\phi^2,\phi)\), and we colored grid-cells green or yellow according to whether they contain a dot or not. Our remaining task was to prove these three facts:

  • Endgame condition: The cell (0,0) is green.
  • Greens lose: From a green cell, there are no other green cells accessible with a single Wythoff’s game move.
  • Yellows win: From any yellow cell, it is possible to move to a green cell with one Wythoff’s game move.
Our guess at the solution to Wythoff's game
Our guess at the solution to Wythoff's game: multiples of vectors v and w (dotted) and their containing cells (dark green).

The “Endgame” condition is easy: the dot at \(0\cdot v = (0,0)\) makes cell (0,0) green. One condition down, two to go!

The “Greens lose” condition asks us to show that no two green cells are in the same row, column, or (slope 1) diagonal—otherwise, you could get from one to the other with a Wythoff move. In fact, we will prove something stronger:

Covering Theorem: Every row, column, and diagonal contains exactly one green cell.

Pictorially, this says that each thick line in the diagrams below will hit one and only one green cell:

Covering the columns and diagonals
All columns (left), diagonals (right), and rows (not pictured) contain exactly one green cell. (Some of these green cells are beyond the image boundaries.) Because the green cell locations are symmetric through the line y=x, the diagram for the rows is redundant and therefore omitted.

It is not difficult to describe why each diagonal is covered, i.e. has exactly one green cell. In the diagram on the right, the central diagonal line has equation \(y-x=0\); the one above it has equation \(y-x=1\); the next is \(y-x=2\); and so on. And because \(\phi^2-\phi=1\), the vector v jumps from one diagonal line to the next at each step. Vector w similarly jumps from line to line in the other direction.

By contrast, I find the fact that each column is covered quite surprising. It says that the upper and lower branches of the “V” perfectly complement each other, each filling exactly the columns that the other skips! Before we prove this fact, let’s see why it helps us.

If we assume the covering theorem for now, we can finish the three conditions needed for our proof. We already saw that (0,0) is green, and the covering theorem certainly tells us that each row, column, and diagonal has at most one green cell, so the “Greens lose” condition holds. We just have to prove the “Yellows win” property: that you can always move to a green cell from any yellow cell. The idea is simple: if your yellow cell is above the “V”[1] then move down to the unique green cell in your column (which may be on either the upper or lower “V” branch). If you are below the “V”, move left to the green cell in your row. Finally, if you are inside the “V”, move diagonally. In this way, you can always move to a green cell with one Wythoff move.

Proving the "Yellows win" condition
All yellow cells can reach a green cell with one Wythoff move. Yellow cells above the "V" can move down to a green cell; yellow cells below the "V" can move left to a green cell; yellow cells inside the "V" can move diagonally to a green cell.

With this third and last property verified, we’re finally done with our proof! …except that we still need to prove the mysterious covering theorem. We’ll discuss this next week. Come back then for the exciting QED!

Notes

  1. i.e., its lower-left corner is above the line \(y=\phi\cdot x\) [↩]

Wythoff’s Formula

Games/Experiments, , ,

Welcome back! I took a few-weeks’ blogging hiatus to focus on end-of-term craziness, but I am now resuming a regular(ish) weekly schedule throughout the summer. Let’s get back to Wythoff’s game!

Here’s a brief recap: In trying to solve for optimal play in Wythoff’s game, we saw how to algorithmically find the blue “losing positions”; we observed that these seemed to lie on two lines and, assuming this fact, we computed the lines’ slopes to be \(\phi\) and \(1/\phi\); and we saw how the Fibonacci numbers were hiding all over the place. But one question lingers: why lines? We’ll answer this today.

Two posts ago, we saw that if we take all of the (infinitely many) steps in the upper “V” branch and average them together, the result has slope \(\phi\). In fact, with a little more work we can compute this “average step” exactly, not just its slope: it is the vector \(v=(\phi,\phi^2)\).[1] Let’s compare these average steps, namely v, 2v, 3v, etc., with the actual ones:

Overlaying average steps on Wythoff's grid
Drawing a dot at each mutliple of the "average" step v reveals a perfect correspondence between dots and blue cells.

The dots and blue squares are perfectly matched! It seems that this may provide a precise way to easily locate all the blue cells in the upper “V” branch at once! And since the whole diagram is symmetric through the line \(y=x\), the lower “V” branch should be governed by vector \(w=(\phi^2,\phi)\) in the same way. Thus, a hypothesis forms:

Conjecture: The losing cells in Wythoff’s game are exactly those that contain an integer multiple of vector \(v=(\phi,\phi^2)\) or vector \(w=(\phi^2,\phi)\).

If we use the notation \(\lfloor x\rfloor\) for the floor function that rounds x down to the nearest integer[2], then this conjecture says that the nth blue cells on the upper and lower “V” branches have coordinates \((\lfloor n\cdot\phi\rfloor, \lfloor n\cdot\phi^2\rfloor)\) and \((\lfloor n\cdot\phi^2\rfloor, \lfloor n\cdot\phi\rfloor)\) respectively. (When \(n=0\), both formulas give (0,0).)

As we will see, this conjecture is indeed correct. How could we rigorously prove this fact?

To start, in a new grid, let’s color green all cells that fit our hypothesized formula, i.e., contain a multiple of v or w. Fill the rest of the cells with yellow. We now have two separate, a priori unrelated colorings of the grid: one with red/blue according to Wythoff’s game, and another with yellow/green according to vectors v and w.

Comparing Wythoff grid colorings
Two colorings of Wythoff's grid that we conjecture are identical. Left: the losing positions (dark blue) found previously by an iterative, optimal-play strategy. Right: multiples of vectors v and w (dotted) and their containing cells (dark green).

Proving the conjecture amounts to showing that these colorings are the same. We’ll accomplish this by showing that the yellow/green coloring behaves just like the red/blue one:

  • Endgame condition: The cell (0,0) is green.
  • Yellows win: From any yellow cell, it is possible to move to a green cell with one Wythoff’s game move.
  • Greens lose: From a green cell, there are no other green cells accessible with a single Wythoff’s game move.

We have already observed these three properties for the red/blue coloring, and we saw that they uniquely determined the red and blue cell positions. If we could show the yellow/green coloring follows the same pattern, we could conclude that the colorings are indeed identical. So we just need to check that our yellow/green formula satisfies these three conditions!

Now that we have set the stage to dig into the meat of this proof, it is time to bid farewell until next week. See you then!

Notes

  1. Indeed, since we know that a=(1,2) and b=(2,3) appear in proportion 1 to \(\phi\), the average step is \(\frac{1}{1+\phi}a+\frac{\phi}{1+\phi}b = (\phi,\phi^2)\). This can also be computed from the Fibonacci observations in the most recent post. [↩]
  2. For example, \(\lfloor 2.718\rfloor = 2\), \(\lfloor 5\rfloor = 5\), and \(\lfloor -3.14\rfloor = -4\). [↩]

The “Fibonacci”est String

Counting/Probability, Games/Experiments, , ,

The celebrated Fibonacci Sequence is defined by setting each term equal to the sum of the two previous terms, starting at \(F_0=0\) and \(F_1=1\). So it continues like this:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …

What’s the relation to last week‘s infinite jump sequence,

a b a b b a b a b b a b b a b a b b a b a b b a b b a b a b b a b b … ?

Let’s find out!

Recall from last week that we can group our sequence into blocks of \(A=(ab)\) and \(B=(abb)\), and that the pattern of “short” and “long” blocks is the same as the pattern of as and bs in the original sequence:

Grouping the Jump Sequence, Level 1 This means we can do this grouping again! Specifically, we can group our sequence into “blocks of blocks”, or level 2 blocks, that look like \(A_2=[(ab)(abb)]\) and \(B_2=[(ab)(abb)(abb)]\):

Grouping the Jump Sequence, Level 2 Furthermore, the pattern of short and long level 2 blocks is still the same as the original jump sequence! So we can keep going, grouping our sequence into level 3 blocks \(A_3=A_2 B_2\) and \(B_3=A_2 B_2 B_2\), level 4 blocks \(A_4=A_3 B_3\) and \(B_4=A_3 B_3 B_3\), and so on, thus finding longer and longer patterns that fill up our sequence. Here’s level 3:

Grouping the Jump Sequence, Level 3 One natural question is: what are the lengths of these blocks? Let’s make a table:

n An Bn An Length Bn Length
0 a b 1 1
1 ab abb 2 3
2 ababb ababbabb 5 8
3 ababbababbabb ababbababbabbababbabb 13 21

The lengths are exactly the Fibonacci numbers! (Prove this!) Furthermore, how many as and bs does each block have? Here’s another table:

n An # of as # of bs Bn # of as # of bs
0 a 1 0 b 0 1
1 ab 1 1 abb 1 2
2 ababb 2 3 ababbabb 3 5
3 ababbababbabb 5 8 ababbababbabbababbabb 8 13

Again the Fibonacci numbers! This gives us another way to compute the ratio of as to bs in the jump sequence: The ratios of bs to as in blocks An and Bn are \(F_{2n}/F_{2n-1}\) and \(F_{2n+1}/F_{2n}\) respectively, so as n gets larger these ratios should both approach last week’s answer, the golden ratio \(\phi\).

OK, so our jump sequence is very “Fibonacci”y: it has blocks of Fibonacci lengths with Fibonacci proportions of as and bs. How can it get any “Fibonacci”er than that? Here’s how: Define a different infinite string using the same definition as the Fibonacci numbers themselves: write \(W_0=0\), \(W_1=1\), and after that, each string is formed by writing the previous two next to each other: \(W_n=W_{n-1}W_{n-2}\). The Ws continue like this:

0, 1, 10, 101, 10110, 10110101, 1011010110110, 101101011011010110101, …,

and in the limit they define some infinite string of 0s and 1s that, without a doubt, is as “Fibonacci”y as it gets. But wait; except for the first digit, this is exactly the same as our jump sequence with 0=a and 1=b!
- 1 0 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 0 1 1 ...
a b a b b a b a b b a b b a b a b b a b a b b a b b a b a b b a b b ... This truly is the Fibonacci numbers reincarnated in a binary string.

A Golden Observation

Counting/Probability, Games/Experiments, Proofs, , ,

Last week we saw that the best strategy for Wythoff’s game is to always move to one of the blue squares in the diagram below (if you can). We found the locations of the blue squares with an iterative algorithm that builds outward from (0,0), but we haven’t yet discovered the underlying pattern in how these blue cells are arranged. Let’s go pattern hunting!

As we noticed last week, the blue cells are arranged in a symmetric “V” shape, formed from two seemingly straight lines. What are the slopes of these lines? This is the question du jour.

Jumps in losing positions for Wythoff's game
Jumps between blue cells for Wythoff's game come in just two sizes: a=(1,2) and b=(2,3).

Looking more carefully, the upper branch of the “V” has only two types of “gaps”: consecutive blue cells are separated by either a “short” (1,2) step (a.k.a. a knight’s move) or a “long” (2,3) step. So, if we believe that this “V” branch is a perfect line, then that line’s slope should be somewhere between the slopes of these two steps, namely \(3/2=1.5\) and \(2/1=2\). Knowing more about how these steps are arranged will tell us more about the “V”.

Specifically, label these “short” and “long” steps as a and b respectively. What we care about is the ratio of bs to as. Why? For example, if there were an equal number of as and bs on average, then the slope of the line would be the same as the vector \(a+b=(3,5)\), i.e., the slope would be 5/3. If there were, say, two bs for each a in the long run, then the line would fall in the direction of \(a+2b=(5,8)\), with slope 8/5. Unfortunately, the ratio we seek is neither 1 nor 2; what is this magic number?

Let’s write down the sequence of jumps along our line. From the diagram above we see that it starts a b a b b a …, and using last week’s iterative algorithm, we can compute farther into this infinite sequence:

a b a b b a b a b b a b b a b a b b a b a b b a b b a b a b b a b b …

This sequence seems to be composed of “blocks” of (a b) and (a b b):

(a b)(a b b)(a b)(a b b)(a b b)(a b)(a b b)(a b)(a b b)(a b b)(a b)(a b b)(a b b)…

So for every a there are either one or two bs, meaning the ratio of bs to as is somewhere between 1 and 2. So the slope should be between 5/3 and 8/5. But what is it exactly? To answer this, we need to know how these “short” and “long” blocks are arranged.

Write A = (a b) and B = (a b b), so we can rewrite the sequence of blocks as

A B A B B A B A B B A B B …

Hold on; this sequence looks familiar. It’s exactly the same pattern as our original jump sequence! So it seems that the pattern of blocks is exactly the same as the pattern of the letters themselves! This is a “self-generating” sequence!

In particular, if the ratio of bs to as is some number r, then the ratio of (a b b) blocks to (a b) blocks is also r. But if we have one block of (a b) and r blocks of (a b b) then we have a total of \(1+2r\) bs and \(1+r\) as, so the ratio of bs to as is \(\frac{1+2r}{1+r}=r\). This simplifies to \(1+r=r^2\), and the solution is the shiny number \(r=\frac{1+\sqrt{5}}{2}\), known as the golden ratio and denoted \(\phi\) (Greek letter phi).

Now we know that our purported line should be in the direction of \(a+b\cdot\phi = (1+2\phi,2+3\phi)\), so the slope is \((2+3\phi)/(1+2\phi)=\phi\). And since our “V” shape is symmetric, the other line should have slope \(1/\phi = \frac{\sqrt{5}-1}{2}\). Done and done!

Well, yes and no. We found the slopes of the lines in the “V”, but why do they form lines at all? And what does all this have to do with the Fibonacci numbers?

Wythoff’s Game: Red or Blue?

Counting/Probability, Games/Experiments, , ,

Let’s play a game; just the two of us. We’ll need a (potentially large!) chess board and a single queen somewhere on the board. We take turns making queen moves, always making progress toward the bottom-left corner of the board. Specifically, in one turn we are allowed to move the queen as far as we want either straight down, straight left, or diagonally down and left (at a 45-degree angle). The first to land the queen on the bottom-left corner wins the game. If you go first and we both play as best as possible, who wins? Well, it depends on where the queen started.

If the queen starts at any of the light-red spaces in the diagram below, you can win on the first move by going straight to the bottom-left corner. On the other hand, if the queen starts at (2,1), then you’re sunk: any move you make lands on a red square and so leaves me in a position to win. So (2,1) is a losing position, indicated by dark blue shading. (The jagged edge reminds us that we could ask the same questions on much bigger grids.)

Wythoff's game: beginning analysis
If the queen starts on a light-red cell, you win on the first move. If she starts on (1,2) or (2,1) (dark blue), you lose.

What should you do if the queen starts at, say, (6,5)? Move to (2,1)! This leaves me in a losing position, so no matter how I respond, you’ll win. So once we find where all the blue losing cells are, your strategy should be: always move to a blue cell, if you can. What if you can only land on red cells? Then you must have started at a blue position, and you’re going to lose.

This also tells us how to find the losing positions, step by step. We know that (2,1) and (1,2) are losing positions, so any position that can reach these in one move is a winning position. But now (3,5) and (5,3) can only reach red cells, so they are blue, and in turn, anything that can directly reach (3,5) or (5,3) is red.

Wythoff's game: continued analysis
Finding blue cells step by step. Left: Because (1,2) and (2,1) are blue, any cells that can reach these directly are red. Right: (3,5) and (5,3) can only reach red cells, so we color them blue. This reveals even more red cells.

Continuing like this, we can fill up our board as follows:

Wythoff's game: completed analysis
Continuing step-by-step as above, all blue cells in the grid are revealed. What patterns can we find?

Interestingly, the blue positions seem to fit nicely into two straight lines forming a “V”-shape, but the exact pattern governing their placement is less clear (especially if we were to ask about larger grids!). Is there more underlying structure in the blue cells’ positioning?[1] How could we discover the pattern in their placement? And why does that line seem to have slope equal to the golden ratio, \(\phi = (1+\sqrt{5})/2\)?[2] Tune in next week to find out! In the meantime, be sure to play a few rounds of Wythoff’s game with your friends!

Notes

  1. Yes. We call that a leading question… [↩]
  2. Correction: that is a leading question. [↩]