[This is post #8 in a mini-blog-post series for NaBloPoMo 2015. Jump to the first, previous, or next post.]
It’s finally time to start building! By the end of this week you’ll have your very own Straws Thingy to keep you company. If you haven’t yet acquired your Target (or other carefully measured [see the previous few posts for details]) straws, now’s the time!
Let’s begin with a simple but immensely helpful step: grab some scissors and cut your straws lengthwise. No, not all the way! Just one slit on the short straw end, and just up to (but not including!) the flexy bits.
This will make it much easier to slide each straw into the next one in future steps. You’ll want to prep 12 straws in each of 5 colors, or 60 straws in all.
If you want to bring some origami back into the project, you can instead make a shallow crease, like this:
Either way, remember that the flexy bits will be visible in the final piece, so avoid cutting or creasing into them.









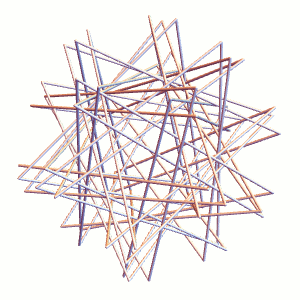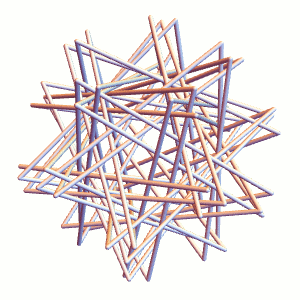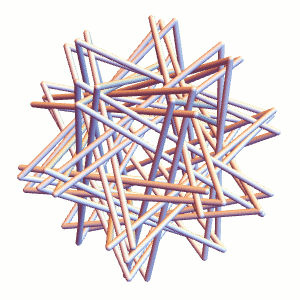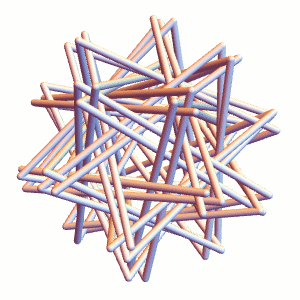











![[Straws Thingy]](http://i1.wp.com/blog.zacharyabel.com/wp-content/uploads/2016/05/straws-thingy-480.jpg?resize=480%2C480)
![[up&up Straws from Target]](http://i0.wp.com/blog.zacharyabel.com/wp-content/uploads/2015/11/up-and-up-straws.jpg?resize=480%2C360)